Binary Search (İkili Arama) Nedir ?
Oldukça popüler bir arama algoritması olan ikili arama sıralı koleksiyonlar üzerinde çalışan bir arama algoritmasıdır. Zaten bir nevi gücünü de verilerin sıralı biçimde olması üzerinden kazanır. Bu nedenle ikili aramayı sırasız bir koleksiyonda kullanmak istersek ilk önce bu koleksiyonun sıralanmasını gerektirir.
Çalışma prensibi olarak arama uzayını azaltmaya dayalı bir yaklaşım benimser. Bu da bu arama tekniğinin hızlı çalışmasında büyük rol oynar.
Algoritmayı okumak yerine izlemeyi tercih ederseniz. Youtube kanalımı ziyaret edebilirsiniz.
Algoritmanın Kodu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public static bool binarySearch(int[] arr, int val) {
int lowerBound = 0;
int upperBound = arr.Length - 1;
while (lowerBound <= upperBound)
{
int mid = (upperBound + lowerBound) / 2;
if (arr[mid] == val)
{
return true;
}
else if (arr[mid] > val)
{
upperBound = mid - 1;
}
else
{
lowerBound = mid + 1;
}
}
return false;
}
Algoritmanın Davranışı
Yukarıdaki kodu birlikte incelemeye başlayalım. Aşağıda arama yapmak istediğimiz koleksiyonumuzu görüyoruz. Burada aradığımız değerinde 11 olduğunu düşünelim.
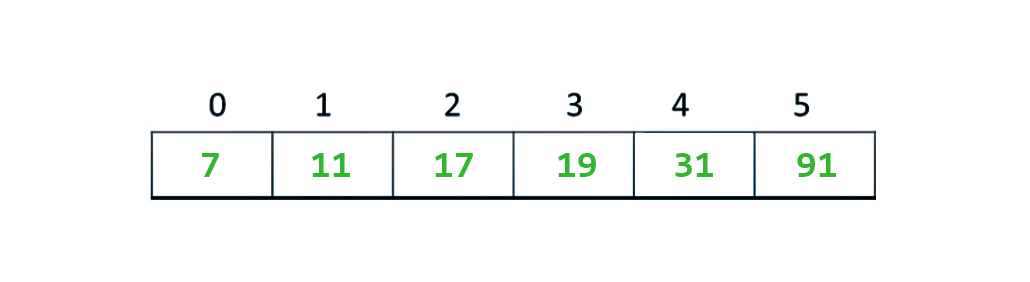
Binary search ilk olarak alt sınırı (lowerBound) ve üst sınırı (upperBound) ifade eden 2 adet işaretçi kullanır.
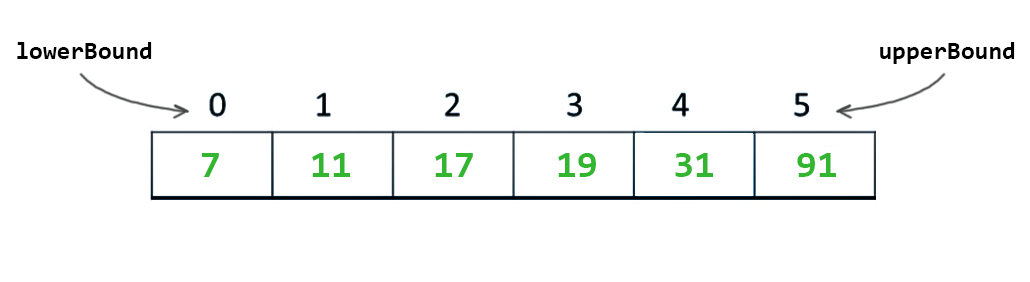
Şimdi bu işaretçileri kullanarak orta nokta (mid) tespiti yapılır.
int mid = (upperBound + lowerBound)/2;
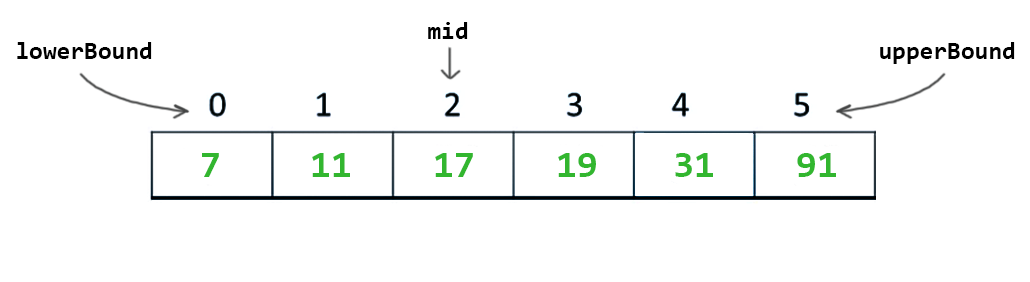
Sonrasında mid deki değer ile aradığımız değer karşılaştırılır.
- middeki değer aradığım ise bulmuşumdur,
- middeki değerden büyük bir değer ise lowerBound u mid + 1 konumuna,
- mid deki değerden küçük ise upperBound u mid - 1 konumuna çekeriz.
Not : Bu bound (sınır) değerlerini oynattığımız anda arama uzayının yarısını elediğimize dikkat edin. (Şimdi neden sıralı koleksiyonları kullandığını görmüşsünüzdür, çünkü koleksiyonun sıralı olduğunu bildiğinden rahatça sınır değerini oynatabiliyor, sıralı olmadığı durumu hayal edin aradığınız değer koleksiyonunuzda olsa bile hiç ulaşamayabilirdiniz.)
Devam edecek olursak, biz 11 i arıyorduk mid deki değer = 17. Dolayısıyla mid den daha küçük bir değer aradığımızdan kesinlikle ben mid in solunda bir konumdayımdır düşüncesi ile üst sınır mid - 1 konumununa çekilir.
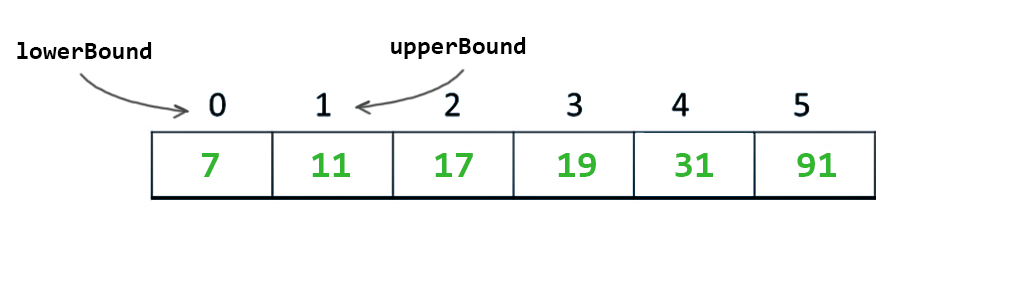
Tekrar mid hesaplanır. int mid = (upperBound + lowerBound)/2; bu sefer 0 konumu yeni mid olur.
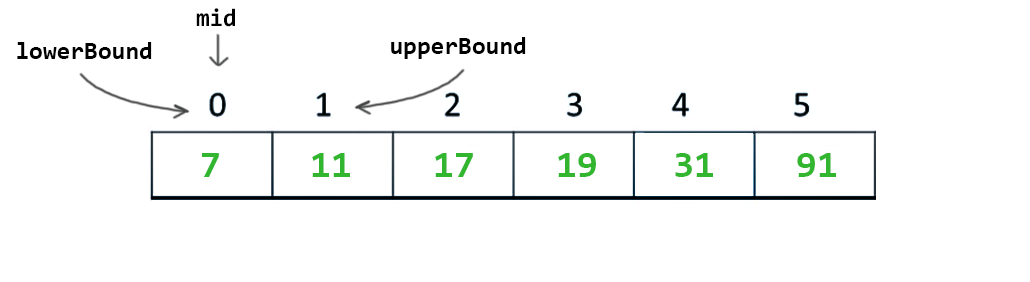
Bu sefer mid deki değer 7 ama benim aradığım 11 idi. Yani mid den büyüğüm. O zaman algoritma kesin ben mid in sağındayımdır düşüncesi ile, lowerBound u mid + 1 konumuna çeker.
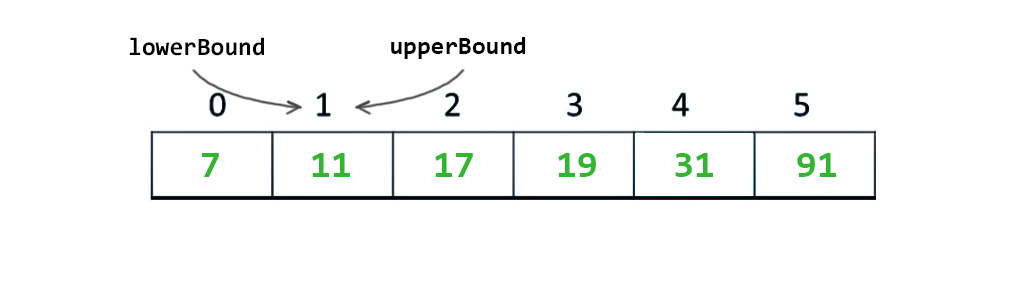
Tekrar mid hesaplanır ve mid = 1 olur ve middeki değerde 11 yani aradığım değer, işte bu kadar aradığımız değeri çok kısa bir sürede bulmuş oluyoruz.
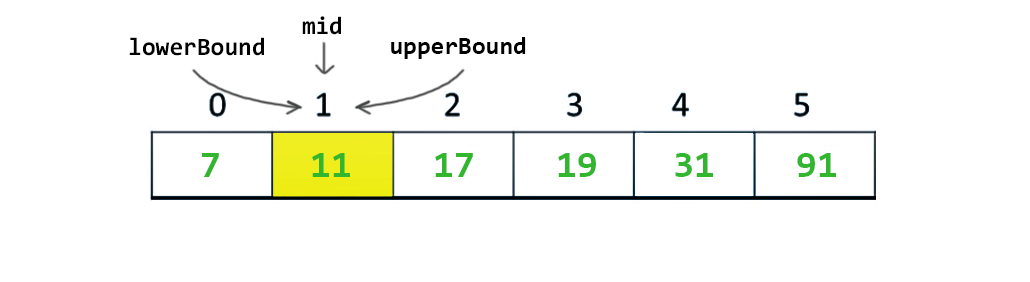
Uyarı : Bu noktada şuna da dikkat edilmesi önemli sınırların kesiştiği nokta son şansımız idi. Eğer bu noktada da bulamasak while (lowerBound <= upperBound) olması sebebiyle döngüyü kıracaktık. Çünkü sınırlar kesiştikten sonra artık arama yapmanın bir anlamı olmayacaktı. Yani diğer bir cümle ile koleksiyonda artık bakılabilecek bir değerin kalmadığı ortaya çıkacaktı. Bizde aranan değerin bu koleksiyonda bulunmadığını dönecektik.
Analiz
Best Case (En iyi durum) : En iyi durum aslında ilk mid değerinin aradığım değer olmasıdır. Yani bir adım O(1) olacaktır.
Worst Case (En kötü durum) : Bu da aslında yukarıdaki örneğimizde de olduğu gibi arama uzayında tek eleman kalıncaya kadar devam ettiğimiz senaryo olacaktır. Algoritma davranışı gereği her sınır değişiminde arama uzayı yarıya indiğinden karmaşıklığıda O(logn) olacaktır.