Jump Search (Atlamalı Arama) Nedir ?
Atlamalı arama algoritması aslında bir nevi linear search varyantı desek yanlış olmaz sanırım. Çünkü algoritma aslında linear search teki karşılaştırma miktarını azaltarak zaman karmaşıklığını düşürmeyi sağlar. Tabi her avantaj kendince bir dezavantajı beraberinde getireceğinden burada da linear search ten farklılaşarak sıralı koleksiyonlar ile çalışmak zorunda kalır. Bu sebeple sırasız koleksiyonların daha önce sıralanmadan jump search ü uygulaması mümkün olmaz.
Algoritmanın Kodu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static bool jumpSearch(int[] arr, int val) {
int blockSize = (int)Math.Sqrt(arr.Length);
int startIndex = 0;
int endIndex = blockSize;
while (endIndex < arr.Length && arr[endIndex] < val) //aradığı değerin bulunduğunu düşündüğü bloğun tespiti
{
startIndex = endIndex;
endIndex += blockSize;
}
if (endIndex >= arr.Length) // blok sınırının taşıp IndexOutOfBound ihtimaline karşı, sınırın son index e çekilmesi
{
endIndex = arr.Length - 1;
}
for (int i = startIndex; i <= endIndex; i++) // linear search yapıldığı nokta
{
if (arr[i] == val)
{
return true;
}
}
return false;
}
Nasıl Çalışır ?
Algoritma, koleksiyonun blok blok şeklinde olduğunu düşünerek hareket eder. Dolayısıyla aradığı eleman bu bloklardan birindedir veya hiçbirinde değildir yani bu koleksiyonda yoktur kanısına varır. Blokları kontrol ederken aradığı elemanın ilgili blokta olduğuna inandığı noktada linear search gerçekleştirir. Bu noktada bulabilirse buldu yoksa aradığı eleman bu koleksiyonda bulunmuyor şeklinde bir sonuca ulaşılır.
Algoritmanın Davranışı
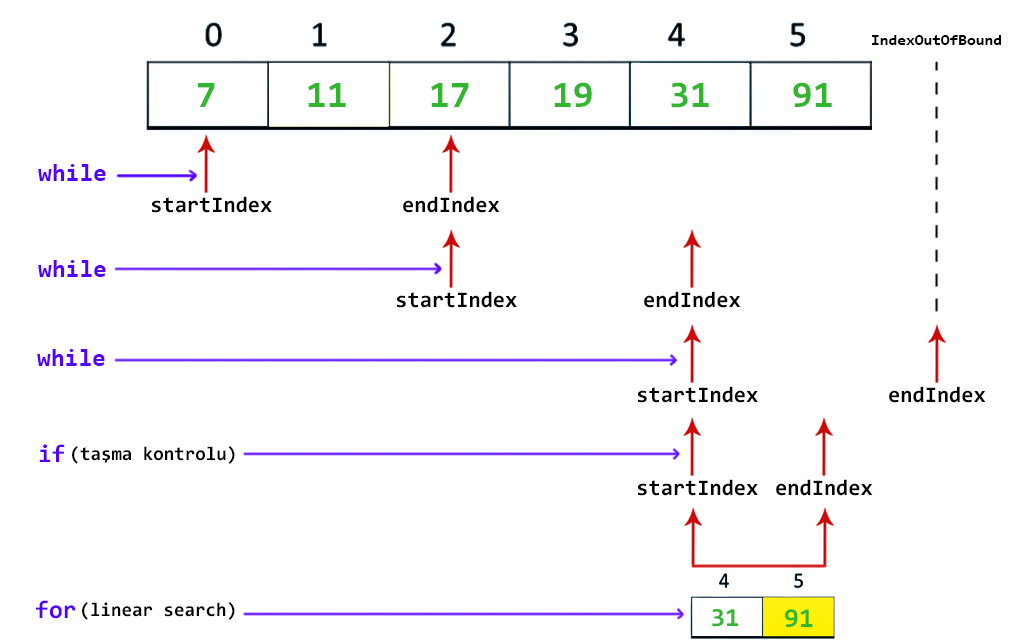
Koleksiyonumuzun aşağıdaki gibi olduğunu düşünelim ve 91 değerini aradığımızı varsayalım.
Block size hesabı
Algoritmanın ilk yaptığı şey bir block size hesaplamak olacaktır. Yukarıda da bahsettiğim gibi aslında bu değer koleksiyonun kaç bloktan oluştuğunu temsil eder. Bu hesabı yapmak için koleksiyonun eleman sayısının karekökünü alır.
Neden karekök ? Çünkü çok uzun atlayışlar yaparsam aradığım değeri aşabiliriz ve geri dönmemiz gerekebilir, çok kısa atlayışlar yaparsamda normal linear search e yakınsarız ve bu aramanın pek bir anlamı kalmaz.
Küçük bir matematik ile √n nin uygunluğunu anlayabiliriz. Koleksiyonumuzun n boyutlu oludğunu ve atlama miktarımızın(block size) x olduğunu düşünelim. En kötü durum senaryosunda yani son bloğun sonuncu index indeki değeri aradığımızı varsayalım. Bizim 91’i aradığımız gibi. Bu durumda n/x atlama yaparız. Ve sonrasında linear search içinde x-1 karşılaştırma gerçekleştiririz.
Sonuç olarak total miktar = n/x + x-1 yapar. Bu kısmı 0 a eşitleyip x’ e göre türev alırsak.
d/dx (n/x + x-1) = -n/x^2 + 1 = 0
x = √n olarak tespit etmiş oluruz. Bu da en kötü durumda en optimum miktarın √n olduğunu gösterir.
İlgili blok tespiti
Block size hesaplandıktan sonra resme dikkatli bakarsanız ilgili bloğu bulmak için 3 kez while döngüsü çalışıyor ve aradığı değerin bulunduğunu düşündüğü(endIndex teki değerin aradığı değerden büyük olduğu veya koleksiyon sınırlarını aşarsa döngüden çıkıyor). Bu noktada neden sıralı koleksiyonlarda çalıştığını fark etmiş olmalısınız. Hatta farkedemediyseniz birkaç dakika bu noktada düşünmenizi tavsiye ederim.
Taşma kontrolu
Bu kısım aslında algoritmanın uygulanış şekline göre değişkenlik gösterebilir, sizlerde internette farklı kaynaklardan araştırmalar yaptığınızda farklı varyantları ile karşılabilirsiniz. Fakat buradaki uyguladığımız şekliyle endIndex imizin koleksiyon sınırını geçip geçmediğine bakıyoruz. Eğer sınırı geçmiş ise koleksiyonumuzun son index ine konuşlandırıyoruz.
Neden son index? Çünkü zaten sınır dışına çıkmış bir index bizim koleksiyonumuzda bakabileceğimiz bir konum değildir. O nedenle koleksiyonumuzda aradığımız değeri bulabileceğimiz son konumu yani son index i atıyoruz.
Ayrıca bu şekilde olası IndexOutOfBound hatasınında önüne geçmiş oluyoruz.
Linear search (Doğrusal Arama)
Son olarak ilgili blok tespiti sonrası blok sınırlarımız [startIndex, endIndex] içerisinde linear search uyguluyoruz. Sonrasında eğer bu aralıkta aradığımız değeri tespit edersek mutlu son, tespit edemezsek aradığımız elemanın bu koleksiyonda olmadığı sonucuna varıyoruz. Yukarıdaki örneğe dönecek olursak [4,5] sınır değerlerine sahip bloğu taradığımızda aradığımız 91 değerinin 5. indexte olduğunu tespit etmiş oluyoruz.
Analiz
Best Case (En iyi durum) : En iyi durumu düşünecek olursak aslında ilk endIndex konumundaki değerin aradığım değer olması olacaktır. Bu durumda O(1) olacaktır.
Worst Case (En kötü durum) : Aradığım değerin koleksiyonun sonundaki değer olduğu durum olacaktır. Block size hesabında √n değerinin optimum olduğunu görmüştük. Şimdi aynı denklemi √n ni yerine koyarak düşünürsek √n atlama + √n - 1 linear search = 2√n - 1 olur. Bu değerde karmaşıklık olarak O(√n) olacaktır.
Buradan yola çıkarak koleksiyonumuz küçük boyutlardaysa aslında bu topa girmek bize ekstra maliyet doğuracağınıda söylemek yanlış olmaz. Direk linear search ten gidilebilmesi daha verimli olacaktır. Öte yandan bir video da belirli bir kareyi tespit etmek içinde jump search kullanmak verimli bir sonuç ortaya çıkarabilir.
Analiz sonucunda algoritmanın karmaşıklık olarak kendisine linear ile binary arasında bir yer bulduğunu söyleyebiliriz. En yavaştan en hızlıya sıralarsak aşağıdaki gibi bir sonuç elde edilecektir.
linear (n) < jump (√n) < binary (logn)