Linear Search (Doğrusal Arama) Nedir ?
Linear search diğer adıyla doğrusal arama aradığımız değeri bir noktadan başlayıp ilgili arama dizesi bitene kadar aramaya devam eden en basit arama algoritmasıdır.
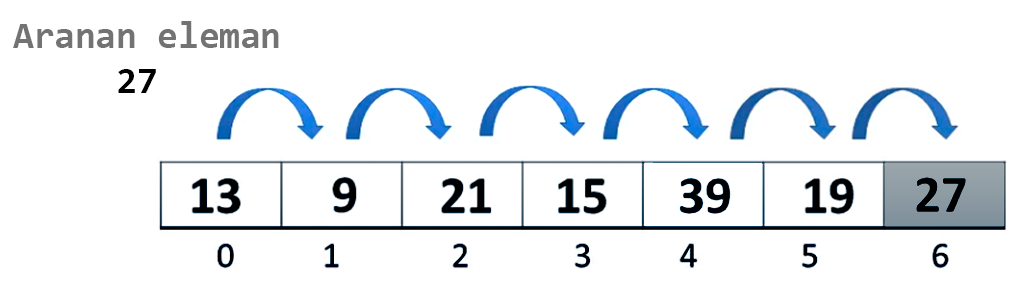
Aşağıda ilgili dizede aranan değer var mı/yok mu ? arayan bir algoritma örneği bulunmaktadır.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static bool linearSearch(int[] arr, int val) {
for (int i = 0; i < arr.Length; i++)
{
if (arr[i] == val)
{
return true;
}
}
return false;
}
// Example:
// bool result = linearSearch(new int[] { 1, 2, 3, 4}, 4);
// val = 4 ilgili dizede bulunduğu için true dönecektir.
Eğer aranan değer var mı ? dan ziyade bulunduğu konumu almak istersek algoritmanın dönüş(return) değerini değiştirerek ilgili konumada ulaşabiliriz.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static int linearSearch(int[] arr, int val) {
for (int i = 0; i < arr.Length; i++)
{
if (arr[i] == val)
{
return i;
}
}
return -1;
}
// Example:
// int result = linearSearch(new int[] { 1, 2, 3, 4}, 4);
// val = 4 ilgili dizede 3. indiste bulunduğu için 3 dönecektir.
Tabi burada şunu farketmek iyi olacaktır. İlgili değer ile ilk karşılaşılan konumu dönecektir. Eğer tüm konumları almak istersek return etmek yerine bir koleksiyonda bu değerleri saklayıp en son bu koleksiyonu geriye dönebiliriz.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static List<int> linearSearch(int[] arr, int value) {
List<int> findIndexes = new List<int>();
for (int i = 0; i < arr.Length; i++)
{
if (arr[i] == value)
{
findIndexes.Add(i);
}
}
return findIndexes;
}
// Example:
// List<int> result = linearSearch(new int[] { 1, 2, 3, 4, 2 ,5}, 2);
// val = 2 ilgili dizede 1. ve 3. indislerde olduğu görünmektedir.
//Dolayısıyla dönen listemizde 1 ve 3 değerleri bulunacaktır.
Not : Örneklere baktığımızda sadece sayılarla çalışıyor gibi anlaşılmasın, farklı veri türlerinde de ilgili yapıyı kurduğunuzda benzer sonuçlara erişebilirsiniz.
Analiz
Best Case (En iyi durum) : En iyi durum aslında sizlerinde tahmin edebileceği gibi aradığımız değerin koleksiyonun ilk değeri olması olacaktır. Bu durumda O(1) olacaktır. Yani bir adımda aradığımız değere ulaşabileceğimizi gösterir.
Worst Case (En kötü durum) : Bu arama için en kötü durumu düşündüğümüzde aslında aradığımız değerin ilgili koleksiyonumuzun sonuncu değeri olması olacaktır. Ve koleksiyonumuzun n boyutunda olduğu düşünülecek olursa bu durumda O(n) olarak karşımıza çıkacaktır.
Bu sonuçlar bize aslında bu algoritmanın büyüyen veri kümelerinde çok kullanılmaması gerektiği yönünde bazı emareler göstermektedir. Çünkü O(n) e baktığımızda koleksiyondaki veri miktarımız ile paralel bir şekilde ulaşım durumumuzda değişmektedir. Bu nedenle nispeden daha az değerle uğraşırken veya büyümeyeceğini düşündüğümüz koleksiyonlarda çalışırken kullanmak daha uygun bir tercih olacaktır.
Farklı bir algoritma yazısında görüşünceye dek kendinize iyi bakın. İyi Çalışmalar